Advanced Placement
Statistics and Probability
Unit 1 & 2
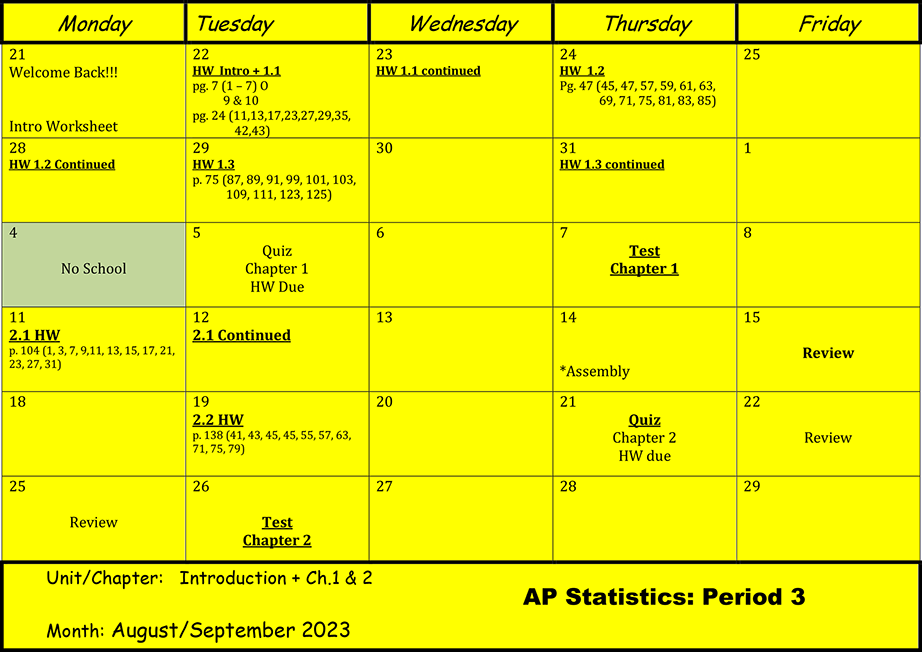
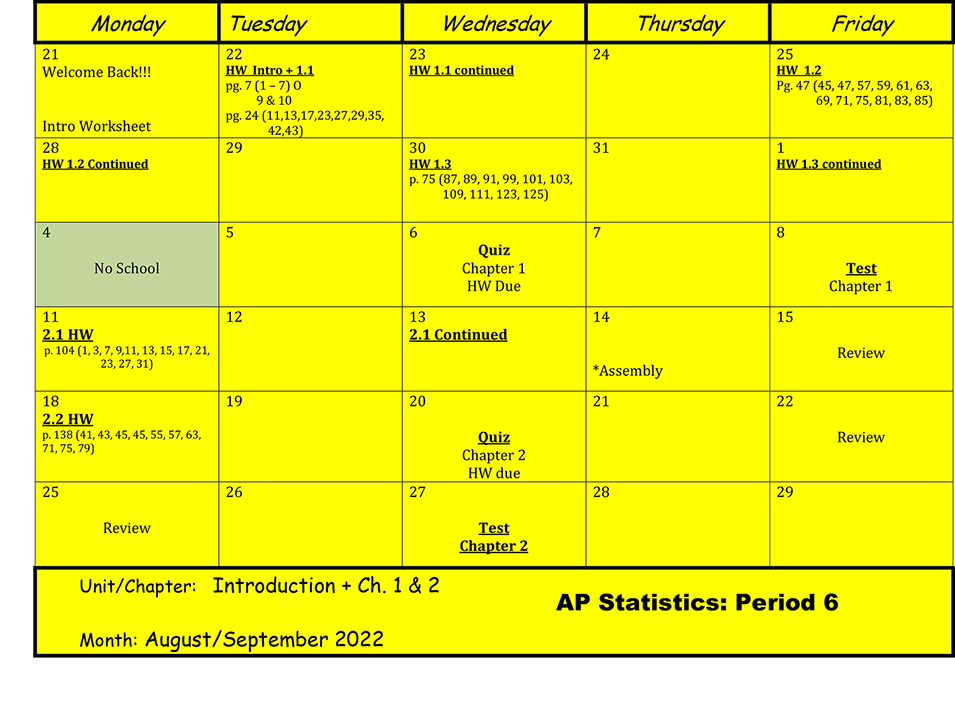
Units 3 & 4
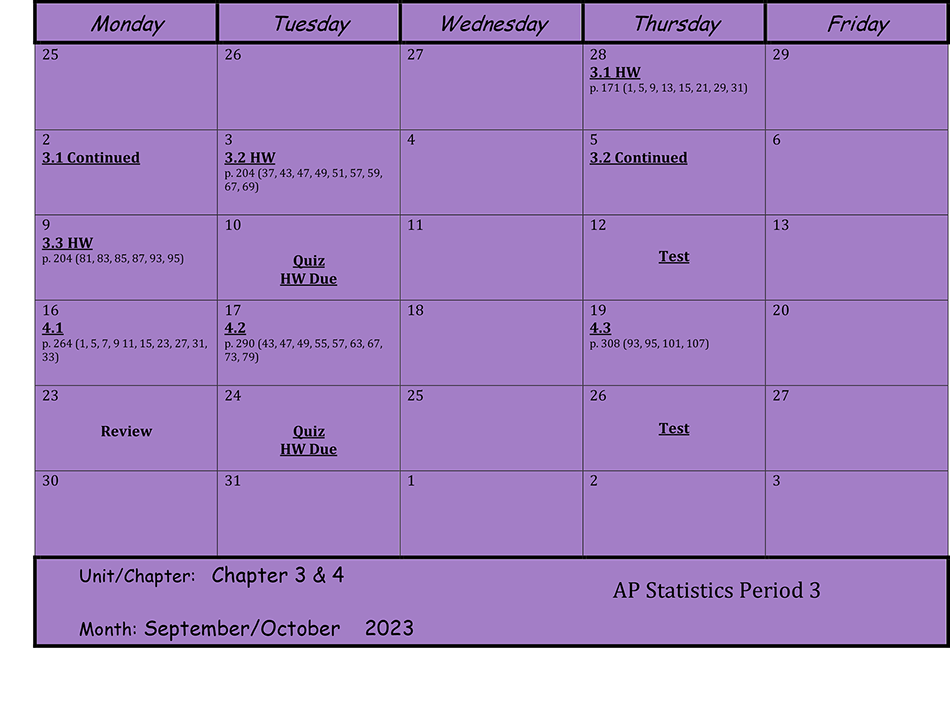
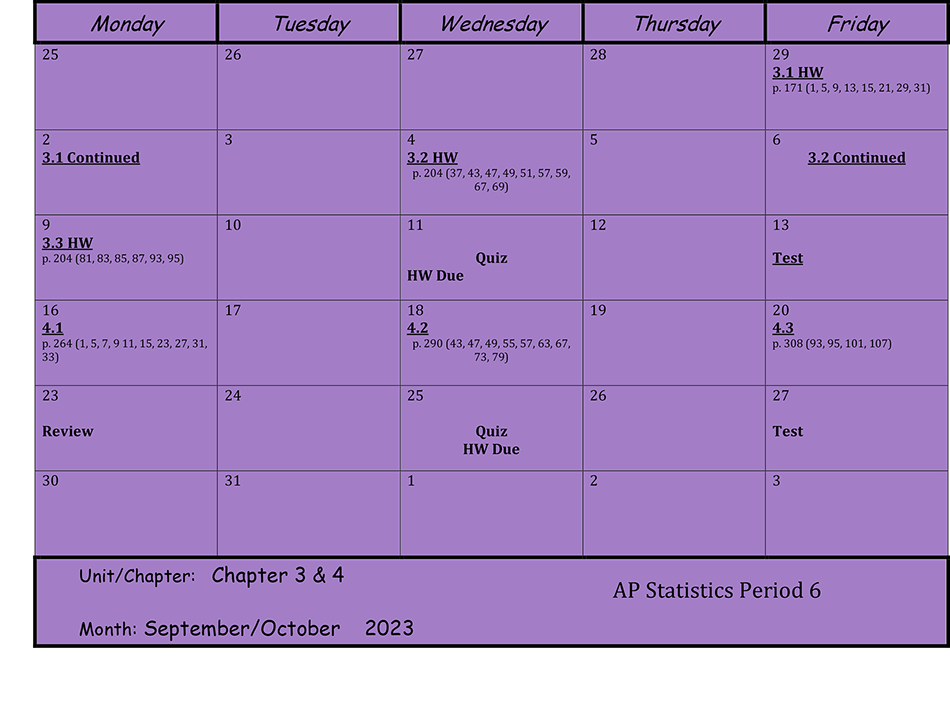
Units 5 & 6
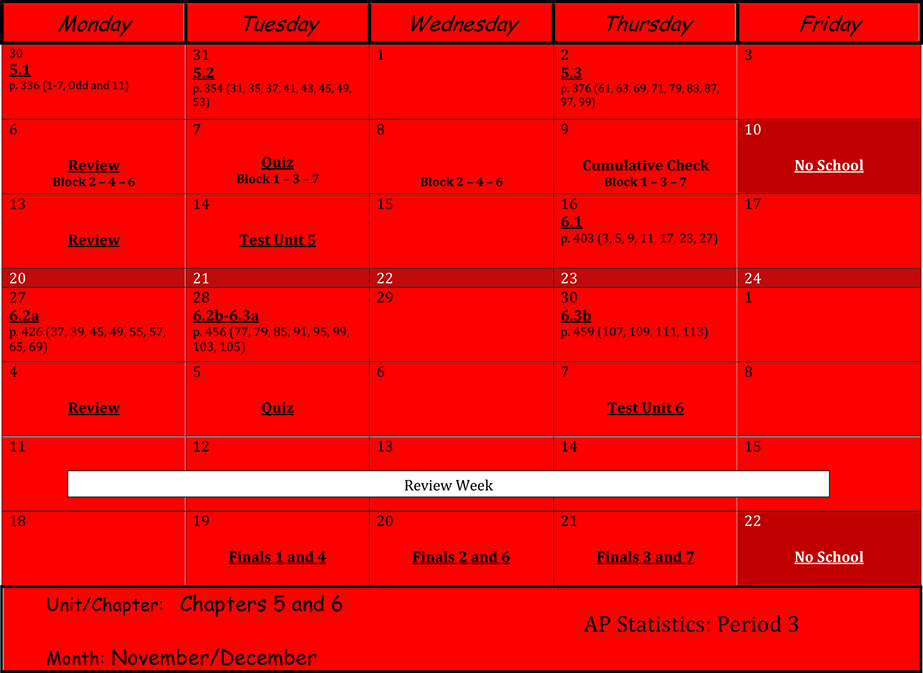
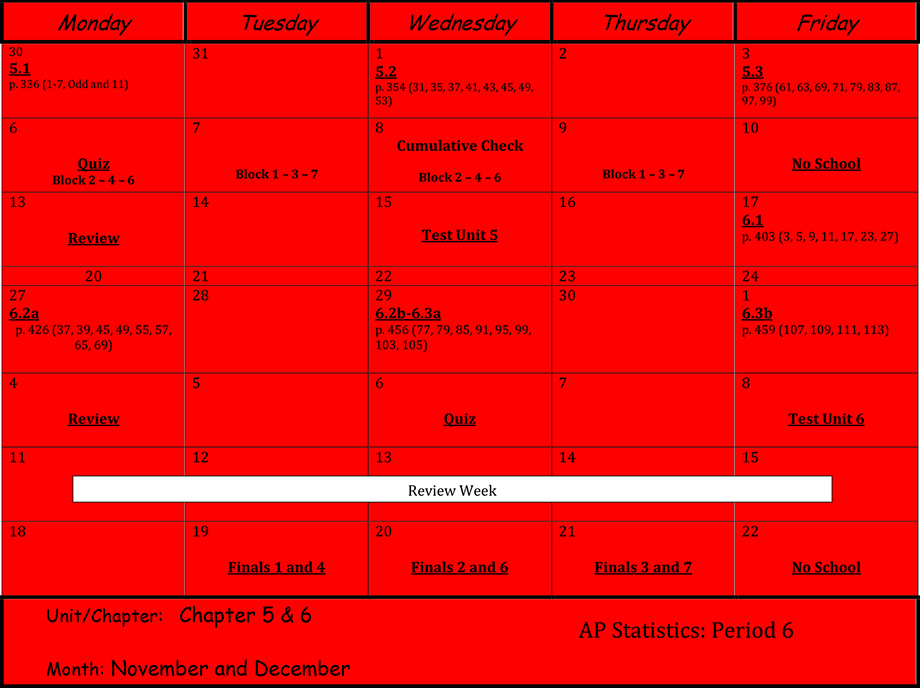
Units 7 & 8
-1.png?crc=453708772)
-2.png?crc=3931447218)
Units 9 - 12a
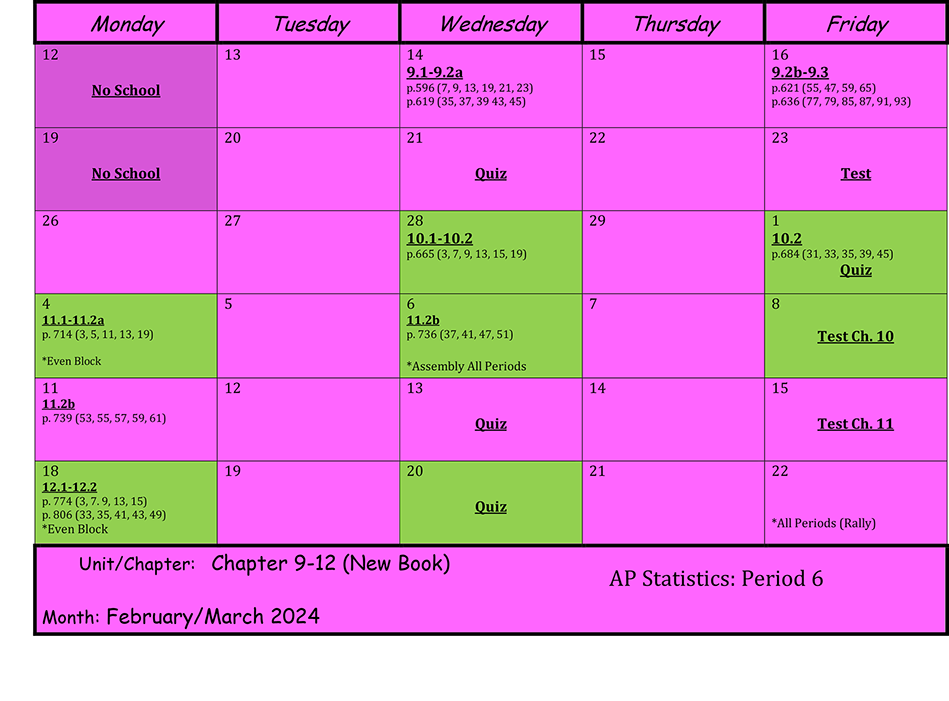
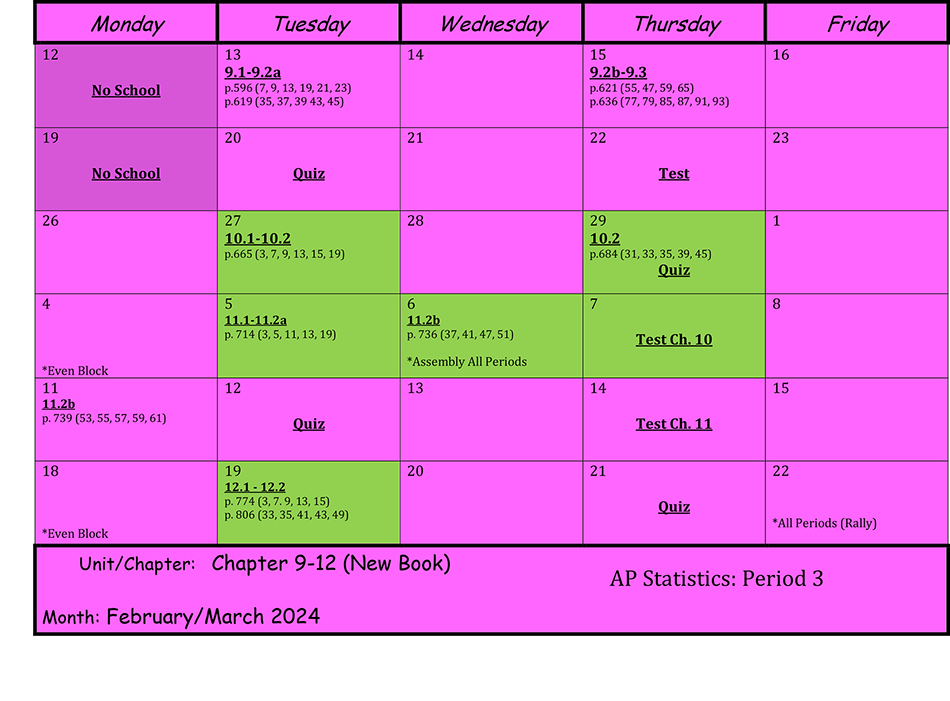
Unit 12b - The End
%202024(1)-1.png?crc=3785908212)
%202024(1)-2-crop-u7636.png?crc=3892367134)
%202024(1)-3.png?crc=4135067401)
%202024(1)-4-crop-u7621.png?crc=428942481)
AP Exam Prep
%202023-3.png?crc=40963916)
%202023-4.png?crc=347283257)
AP Statistics
Syllabus
Advanced Placement
Statistics and Probability
Unit 1 & 2


Units 3 & 4


Units 5 & 6


Units 7 & 8
-1.png?crc=453708772)
-2.png?crc=3931447218)
Units 9 - 12a


Unit 12b - The End
%202024(1)-1.png?crc=3785908212)
%202024(1)-2-crop-u7636.png?crc=3892367134)
%202024(1)-3.png?crc=4135067401)
%202024(1)-4-crop-u7621.png?crc=428942481)
AP Exam Prep
%202023-3.png?crc=40963916)
%202023-4.png?crc=347283257)
AP Statistics
Syllabus